Description
ShinyItemAnalysis
provides analysis of educational tests (such as admission tests)
and their items including:
- Exploration of total and standard scores on Summary page.
- Item and distractor analysis on Traditional Analysis page.
- Item analysis by logistic models on Regression page.
- Item analysis by item response theory models on IRT models page.
- Differential item functioning (DIF) and differential distractor functioning (DDF) methods on DIF/Fairness page.
This application is based on the free statistical software R and its Shiny package.
For all graphical outputs a download button is provided. Moreover, on Reports page HTML or PDF report can be created. Additionaly, all application outputs are complemented by selected R code hence the similar analysis can be run and modified in R.
You can also download
ShinyItemAnalysis
package from
CRAN
to use it offline or run it faster.
Data
For demonstration purposes, by default, 20-item dataset
GMAT
from R
difNLR
package is used. Other three datasets are available:
GMAT2
and
Medical 20 DIF
from
difNLR
package and
Medical 100
from
ShinyItemAnalysis
package.
You can change the dataset (and try your own one) on page
Data.
Version
Current version of
ShinyItemAnalysis
is 1.1.0
List of packages used
library(corrplot)
library(CTT)
library(deltaPlotR)
library(DT)
library(difNLR)
library(difR)
library(ggplot2)
library(grid)
library(gridExtra)
library(latticeExtra)
library(ltm)
library(mirt)
library(moments)
library(msm)
library(nnet)
library(psych)
library(psychometric)
library(reshape2)
library(rmarkdown)
library(shiny)
library(shinyjs)
library(stringr)
library(WrightMap)
Authors

Patricia Martinkova, Institute of Computer Science, Czech Academy of Sciences

Adela Drabinova


Jakub Houdek
Bug reports
If you discover a problem with this application please contact the project maintainer at martinkova(at)cs.cas.cz or use GitHub.
Acknowledgments
Project was supported by grant funded by Czech Science foundation under number GJ15-15856Y.
License
Copyright 2016 Patricia Martinkova, Adela Drabinova, Ondrej Leder and Jakub Houdek
This program is free software you can redistribute it and or modify it under the terms of the GNU General Public License as published by the Free Software Foundation either version 3 of the License or at your option any later version.
This program is distributed in the hope that it will be useful, but WITHOUT ANY WARRANTY; without even the implied warranty of MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the GNU General Public License for more details.
Data
For demonstration purposes, 20-item dataset
GMAT
and dataset
GMATkey
from R
difNLR
package are used.
On this page, you may select one of four datasets offered from
difNLR
and
ShinyItemAnalysis
packages or you may upload your own dataset
(see below). To return to demonstration dataset,
refresh this page in your browser
(F5)
.
Used dataset
GMAT
is generated based on parameters of real Graduate Management
Admission Test (GMAT) data set (Kingston et al., 1985). However, first two items were
generated to function differently in uniform and non-uniform way respectively.
The data set represents responses of 2,000 subjects (1,000 males, 1,000 females) to
multiple-choice test of 20 items. The distribution of total scores is the same for both groups.
Dataset
GMAT2
is also generated based on parameters of GMAT (Kingston et
al., 1985) from R
difNLR
package . Again, first two items were generated
to function differently in uniform and non-uniform way respectively. The data set
represents responses of 1,000 subjects (500 males, 500 females) to multiple-choice test
of 20 items.
Dataset
Medical 20 DIF
is a subset of real admission test to medical
school from R
difNLR
package. First item was previously detected as
functioning differently. The data set represents responses of 1,407 subjects (484 males,
923 females) to multiple-choice test of 20 items. For more details of item selection
see Drabinova & Martinkova (2016).
Dataset
Medical 100
is a real data set of admission test to medical school
from R
ShinyItemAnalysis
package . The data set represents responses of
3,204 subjects to multiple-choice test of 100 items. There is no group membership
variable in the data set hence it is not possible to run DIF or DDF detection procedures.
Upload your own datasets
Main dataset should contain responses of individual students (rows) to given items (columns). Header may contain item names, no row names should be included. If responses are in unscored ABCD format, the key provides correct response for each item. If responses are scored 0-1, key is vector of 1s. Group is 0-1 vector, where 0 represents reference group and 1 represents focal group. Its length need to be the same as number of individual students in main dataset. If the group is not provided then it wont be possible to run DIF and DDF detection procedures. In all data sets header should be either included or excluded.
Data specification
Data check
Key (correct answers)
Scored test
Group vector
Analysis of total scores
Summary table
Histogram of total score
For selected cut-score, blue part of histogram shows students with total score above the cut-score, grey column shows students with Total Score equal to cut-score and red part of histogram shows students below the cut-score.
Download figureSelected R code
library(difNLR)
data(GMAT)
data <- GMAT[, colnames(GMAT) != "group"]
score <- apply(data, 1, sum) # Total score
# Summary of total score
summary(score)
# Histogram
hist(score, breaks = 0:ncol(data))
Standard scores
Total Score
also known as raw score is a total number of correct
answers. It can be used to compare individual score to a norm group, e.g. if the mean
is 12, then individual score can be compared to see if it is below or above this average.
Percentile
indicates the value below which a percentage of observations
falls, e.g. a individual score at the 80th percentile means that the individual score
is the same or higher than the scores of 80% of all respondents.
Success Rate
is the percentage of success, e.g. if the maximum points of test
is equal to 20 and individual score is 12 then success rate is 12/20 = 0.6, i.e. 60%.
Z-score
or also standardized score is a linear transformation of total
score with a mean of 0 and with variance of 1. If X is total score, M its mean and SD its
standard deviation then Z-score = (X - M) / SD.
T-score
is transformed Z-score with a mean of 50 and standard deviation
of 10. If Z is Z-score then T-score = (Z * 10) + 50.
Table by score
Selected R code
library(difNLR)
data(GMAT)
data <- GMAT[, colnames(GMAT) != "group"]
score <- apply(data, 1, sum) # Total score
tosc <- sort(unique(score)) # Levels of total score
perc <- cumsum(prop.table(table(score))) # Percentiles
sura <- 100 * (tosc / max(score)) # Success rate
zsco <- sort(unique(scale(score))) # Z-score
tsco <- 50 + 10 * zsco # T-score
Correlation structure
Polychoric correlation heat map
Polychoric correlation heat map is a correlation plot which displays a polychoric correlations of items. The size and shade of circles indicate how much the items are correlated (larger and darker circle means larger correlation). The color of circles indicates in which way the items are correlated - blue color shows possitive correlation and red color shows negative correlation.
Download figureScree plot
A scree plot displays the eigenvalues associated with an component or a factor in descending order versus the number of the component or factor.
Download figureSelected R code
library(corrplot)
library(difNLR)
library(psych)
data(GMAT)
data <- GMAT[, colnames(GMAT) != "group"]
# Correlation plot
corP <- polychoric(data)
corrplot(corP$rho)
corP$rho # Correlation matrix
# Scree plot
plot(1:length(eigen(corP$rho)$values), eigen(corP$rho)$values,
ylab = "Eigen value", xlab = "Component Number")
lines(1:length(eigen(corP$rho)$values), eigen(corP$rho)$values)
eigen(corP$rho) # Eigen values and vectors
Traditional item analysis
Traditional item analysis uses proportions of correct answers or correlations to estimate item properties.
Item difficulty/discrimination graph
Displayed is difficulty (red) and discrimination (blue)
for all items. Items are ordered by difficulty.
Difficulty
of items is estimated as percent of students who
answered correctly to that item.
Discrimination
is described by difference of percent correct
in upper and lower third of students (Upper-Lower Index, ULI). By rule of
thumb it should not be lower than 0.2 (borderline in the plot), except for
very easy or very difficult items.
Cronbach's alpha
Chronbach's alpha is an estimate of the reliability of a psychometric test. It is a function of the number of items in a test, the average covariance between item-pairs, and the variance of the total score (Cronbach, 1951).
Traditional item analysis table
Explanation: Difficulty - Difficulty of item is estimated as percent of students who answered correctly to that item. SD - standard deviation, RIT - Pearson correlation between item and Total score, RIR - Pearson correlation between item and rest of items, ULI - Upper-Lower Index, Alpha Drop - Cronbach's alpha of test without given item.
Selected R code
library(difNLR)
library(psych)
library(psychometric)
library(ShinyItemAnalysis)
data(GMAT)
data <- GMAT[, colnames(GMAT) != "group"]
# Difficulty and discrimination plot
DDplot(data)
# Cronbach alpha
psych::alpha(data)
# Table
tab <- round(data.frame(item.exam(data, discr = TRUE)[, c(4, 1, 5, 2, 3)],
psych::alpha(data)$alpha.drop[, 1]), 2)
colnames(tab) <- c("Difficulty", "SD", "Dsicrimination ULI", "Discrimination RIT", "Discrimination RIR", "Alpha Drop")
tab
Distractor analysis
In distractor analysis, we are interested in how test takers select the correct answer and how the distractors (wrong answers) were able to function effectively by drawing the test takers away from the correct answer.
Distractors plot
Table with counts
Table with proportions
Histogram of total scores
Download figureTable of total scores by groups
Selected R code
library(difNLR)
library(ShinyItemAnalysis)
data(GMATtest)
data <- GMATtest[, colnames(GMATtest) != "group"]
data(GMATkey)
key <- GMATkey
# Combinations - plot for item 1 and 3 groups
plotDistractorAnalysis(data, key, num.group = 3, item = 1,
multiple.answers = T)
# Distractors - plot for item 1 and 3 groups
plotDistractorAnalysis(data, key, num.group = 3, item = 1,
multiple.answers = F)
# Table with counts and margins - item 1 and 3 groups
DA <- DistractorAnalysis(data, key, num.groups = 3)[[1]]
dcast(as.data.frame(DA), response ~ score.level, sum, margins = T, value.var = "Freq")
# Table with proportions - item 1 and 3 groups
DistractorAnalysis(data, key, num.groups = 3, p.table = T)[[1]]
tab
Logistic regression on total scores
Various regression models may be fitted to describe item properties in more detail. Logistic regression can model dependency of probability of correct answer on total score by s-shaped logistic curve. Parameter b0 describes horizontal position of the fitted curve, parameter b1 describes its slope.
Plot with estimated logistic curve
Points represent proportion of correct answer with respect to total score. Their size is determined by count of respondents who answered item correctly.
Equation
$$\mathrm{P}(Y = 1|X, b_0, b_1) = \mathrm{E}(Y|X, b_0, b_1) = \frac{e^{\left( b_{0} + b_1 X\right)}}{1+e^{\left( b_{0} + b_1 X\right) }} $$Table of parameters
Selected R code
library(difNLR)
data(GMAT)
data <- GMAT[, colnames(GMAT) != "group"]
score <- apply(data, 1, sum)
# Logistic model for item 1
fit <- glm(data[, 1] ~ score, family = binomial)
# Coefficients
coef(fit)
# Function for plot
fun <- function(x, b0, b1){exp(b0 + b1 * x) / (1 + exp(b0 + b1 * x))}
# Plot of estimated curve
curve(fun(x, b0 = coef(fit)[1], b1 = coef(fit)[2]), 0, 20,
xlab = "Total score",
ylab = "Probability of correct answer",
ylim = c(0, 1))
Logistic regression on standardized total scores
Various regression models may be fitted to describe item properties in more detail. Logistic regression can model dependency of probability of correct answer on standardized total score (Z-score) by s-shaped logistic curve. Parameter b0 describes horizontal position of the fitted curve (difficulty), parameter b1 describes its slope at inflection point (discrimination).
Plot with estimated logistic curve
Points represent proportion of correct answer with respect to standardized total score. Their size is determined by count of respondents who answered item correctly.
Equation
$$\mathrm{P}(Y = 1|Z, b_0, b_1) = \mathrm{E}(Y|Z, b_0, b_1) = \frac{e^{\left( b_{0} + b_1 Z\right) }}{1+e^{\left( b_{0} + b_1 Z\right) }} $$Table of parameters
Selected R code
library(difNLR)
data(GMAT)
data <- GMAT[, colnames(GMAT) != "group"]
stand.score <- scale(apply(data, 1, sum))
# Logistic model for item 1
fit <- glm(data[, 1] ~ stand.score, family = binomial)
# Coefficients
coef(fit)
# Function for plot
fun <- function(x, b0, b1){exp(b0 + b1 * x) / (1 + exp(b0 + b1 * x))}
# Plot of estimated curve
curve(fun(x, b0 = coef(fit)[1], b1 = coef(fit)[2]), -3, 3,
xlab = "Standardized total score",
ylab = "Probability of correct answer",
ylim = c(0, 1))
Logistic regression on standardized total scores with IRT parameterization
Various regression models may be fitted to describe item properties in more detail. Logistic regression can model dependency of probability of correct answer on standardized total score (Z-score) by s-shaped logistic curve. Note change in parametrization - the IRT parametrization used here corresponds to the parametrization used in IRT models. Parameter b describes horizontal position of the fitted curve (difficulty), parameter a describes its slope at inflection point (discrimination).
Plot with estimated logistic curve
Points represent proportion of correct answer with respect to standardized total score. Their size is determined by count of respondents who answered item correctly.
Equation
$$\mathrm{P}(Y = 1|Z, a, b) = \mathrm{E}(Y|Z, a, b) = \frac{e^{ a\left(Z - b\right) }}{1+e^{a\left(Z - b\right)}} $$Table of parameters
Selected R code
library(difNLR)
data(GMAT)
data <- GMAT[, colnames(GMAT) != "group"]
stand.score <- scale(apply(data, 1, sum))
# Logistic model for item 1
fit <- glm(data[, 1] ~ stand.score, family = binomial)
# Coefficients - tranformation
coef <- c(a = coef(fit)[2], b = - coef(fit)[1] / coef(fit)[2])
coef
# Function for plot
fun <- function(x, a, b){exp(a * (x - b)) / (1 + exp(a * (x - b)))}
# Plot of estimated curve
curve(fun(x, a = coef[1], b = coef[2]), -3, 3,
xlab = "Standardized total score",
ylab = "Probability of correct answer",
ylim = c(0, 1))
Nonlinear regression on standardized total scores
Various regression models may be fitted to describe item properties in more detail. Nonlinear regression can model dependency of probability of correct answer on standardized total score (Z-score) by s-shaped logistic curve. The IRT parametrization used here corresponds to the parametrization used in IRT models. Parameter b describes horizontal position of the fitted curve (difficulty), parameter a describes its slope at inflection point (discrimination). This model allows for nonzero lower left asymptote c (pseudo-guessing).
Plot with estimated nonlinear curve
Points represent proportion of correct answer with respect to standardized total score. Their size is determined by count of respondents who answered item correctly.
Equation
$$\mathrm{P}(Y = 1|Z, b_0, b_1, c) = \mathrm{E}(Y|Z, b_0, b_1, c) = c + \left( 1-c \right) \cdot \frac{e^{a\left(Z-b\right) }}{1+e^{a\left(Z-b\right) }} $$Table of parameters
Selected R code
library(difNLR)
data(GMAT)
Data <- GMAT[, colnames(GMAT) != "group"]
stand.score <- scale(apply(Data, 1, sum))
# NLR model for item 1
fun <- function(x, a, b, c){c + (1 - c) * exp(a * (x - b)) / (1 + exp(a * (x - b)))}
fit <- nls(data[, 1] ~ fun(stand.score, a, b, c), algorithm = "port",
start = startNLR(data, GMAT[, "group"], model = "3PLcg")[1, 1:3])
# Coefficients
coef(fit)
# Plot of estimated curve
curve(fun(x, a = coef(fit)[1], b = coef(fit)[2], c = coef(fit)[3]), -3, 3,
xlab = "Standardized total score",
ylab = "Probability of correct answer",
ylim = c(0, 1))
Logistic regression model selection
Here you can compare classic 2PL logistic regression model to non-linear model item by item using some information criterions:
- AIC is the Akaike information criterion (Akaike, 1974),
- BIC is the Bayesian information criterion (Schwarz, 1978)
Another approach to nested models can be likelihood ratio chi-squared test. Significance level is set to 0.05. As tests are performed item by item, it is possible to use multiple comparison correction method.
Table of comparison statistics
Rows BEST indicate which model has the lowest value of criterion, or is the largest significant model by likelihood ratio test.
Selected R code
library(difNLR)
data(GMAT)
Data <- GMAT[, colnames(GMAT) != "group"]
stand.score <- scale(apply(Data, 1, sum))
# Fitting models
fun <- function(x, a, b, c){c + (1 - c) * exp(a * (x - b)) / (1 + exp(a * (x - b)))}
# 2PL model for item 1
fit2PL <- nls(Data[, 1] ~ fun(stand.score, a, b, c = 0), algorithm = "port",
start = startNLR(Data, GMAT[, "group"], model = "3PLcg")[1, 1:2])
# 3PL model for item 1
fit3PL <- nls(Data[, 1] ~ fun(stand.score, a, b, c), algorithm = "port",
start = startNLR(Data, GMAT[, "group"], model = "3PLcg")[1, 1:3])
# Comparison
AIC(fit2PL); AIC(fit3PL)
BIC(fit2PL); BIC(fit3PL)
LRstat <- -2 * (sapply(fit2PL, logLik) - sapply(fit3PL, logLik))
LRdf <- 1
LRpval <- 1 - pchisq(LRstat, LRdf)
LRpval <- p.adjust(LRpval, method = "BH")
Multinomial regression on standardized total scores
Various regression models may be fitted to describe item properties in more detail. Multinomial regression allows for simultaneous modelling of probability of choosing given distractors on standardized total score (Z-score).
Plot with estimated curves of multinomial regression
Points represent proportion of selected option with respect to standardized total score. Their size is determined by count of respondents who selected given option.
Equation
Table of parameters
Selected R code
library(difNLR)
library(nnet)
data(GMAT)
data.scored <- GMAT[, colnames(GMAT) != "group"]
stand.score <- scale(apply(data, 1, sum))
data(GMATtest)
data <- GMATtest[, colnames(GMATtest) != "group"]
data(GMATkey)
key <- GMATkey
# multinomial model for item 1
fit <- multinom(relevel(data[, 1], ref = paste(key[1])) ~ stand.score)
# Coefficients
coef(fit)
One parameter Item Response Theory model
Item Response Theory (IRT) models are mixed-effect regression models in which student ability (theta) is assumed to be a random effect and is estimated together with item paramters. Ability (theta) is often assumed to follow normal distibution.
In 1PL IRT model, all items are assumed to have the same slope in inflection point – the same discrimination a. Items can differ in location of their inflection point – in item difficulty b. More restricted version of this model, the Rasch model, assumes discrimination a is equal to 1.
Equation
$$\mathrm{P}\left(Y_{ij} = 1\vert \theta_{i}, a, b_{j} \right) = \frac{e^{a\left(\theta_{i}-b_{j}\right) }}{1+e^{a\left(\theta_{i}-b_{j}\right) }} $$Item characteristic curves
Download figureItem information curves
Download figureTest information function
Download figureTable of parameters
Scatter plot of factor scores and standardized total scores
Download figureSelected R code
library(difNLR)
library(ltm)
data(GMAT)
data <- GMAT[, colnames(GMAT) != "group"]
# Model
fit <- rasch(data)
# for Rasch model use
# fit <- rasch(data, constraint = cbind(ncol(data) + 1, 1))
# Item Characteristic Curves
plot(fit)
# Item Information Curves
plot(fit, type = "IIC")
# Test Information Function
plot(fit, items = 0, type = "IIC")
# Coefficients
coef(fit)
# Factor scores vs Standardized total scores
df1 <- ltm::factor.scores(fit, return.MIvalues = T)$score.dat
FS <- as.vector(df1[, "z1"])
df2 <- df1
df2$Obs <- df2$Exp <- df2$z1 <- df2$se.z1 <- NULL
STS <- as.vector(scale(apply(df2, 1, sum)))
df <- data.frame(FS, STS)
plot(FS ~ STS, data = df,
xlab = "Standardized total score",
ylab = "Factor score")
Two parameter Item Response Theory model
Item Response Theory (IRT) models are mixed-effect regression models in which student ability (theta) is assumed to be a random effect and is estimated together with item paramters. Ability (theta) is often assumed to follow normal distibution.
2PL IRT model, allows for different slopes in inflection point – different discriminations a. Items can also differ in location of their inflection point – in item difficulty b.
Equation
$$\mathrm{P}\left(Y_{ij} = 1\vert \theta_{i}, a_{j}, b_{j}\right) = \frac{e^{a_{j}\left(\theta_{i}-b_{j}\right) }}{1+e^{a_{j}\left(\theta_{i}-b_{j}\right) }} $$Item characteristic curves
Download figureItem information curves
Download figureTest information function
Download figureTable of parameters
Scatter plot of factor scores and standardized total scores
Download figureSelected R code
library(difNLR)
library(ltm)
data(GMAT)
data <- GMAT[, colnames(GMAT) != "group"]
# Model
fit <- ltm(data ~ z1, IRT.param = TRUE)
# Item Characteristic Curves
plot(fit)
# Item Information Curves
plot(fit, type = "IIC")
# Test Information Function
plot(fit, items = 0, type = "IIC")
# Coefficients
coef(fit)
# Factor scores vs Standardized total scores
df1 <- ltm::factor.scores(fit, return.MIvalues = T)$score.dat
FS <- as.vector(df1[, "z1"])
df2 <- df1
df2$Obs <- df2$Exp <- df2$z1 <- df2$se.z1 <- NULL
STS <- as.vector(scale(apply(df2, 1, sum)))
df <- data.frame(FS, STS)
plot(FS ~ STS, data = df,
xlab = "Standardized total score",
ylab = "Factor score")
Three parameter Item Response Theory model
Item Response Theory (IRT) models are mixed-effect regression models in which student ability (theta) is assumed to be a random effect and is estimated together with item paramters. Ability (theta) is often assumed to follow normal distibution.
3PL IRT model, allows for different discriminations of items a, different item difficulties b, and allows also for nonzero left asymptote – pseudo-guessing c.
Equation
$$\mathrm{P}\left(Y_{ij} = 1\vert \theta_{i}, a_{j}, b_{j}, c_{j} \right) = c_{j} + \left(1 - c_{j}\right) \cdot \frac{e^{a_{j}\left(\theta_{i}-b_{j}\right) }}{1+e^{a_{j}\left(\theta_{i}-b_{j}\right) }} $$Item characterisic curves
Download figureItem information curves
Download figureTest information function
Download figureTable of parameters
Scatter plot of factor scores and standardized total scores
Download figureSelected R code
library(difNLR)
library(ltm)
data(GMAT)
data <- GMAT[, colnames(GMAT) != "group"]
# Model
fit <- tpm(data, IRT.param = TRUE)
# Item Characteristic Curves
plot(fit)
# Item Information Curves
plot(fit, type = "IIC")
# Test Information Function
plot(fit, items = 0, type = "IIC")
# Coefficients
coef(fit)
# Factor scores vs Standardized total scores
df1 <- ltm::factor.scores(fit, return.MIvalues = T)$score.dat
FS <- as.vector(df1[, "z1"])
df2 <- df1
df2$Obs <- df2$Exp <- df2$z1 <- df2$se.z1 <- NULL
STS <- as.vector(scale(apply(df2, 1, sum)))
df <- data.frame(FS, STS)
plot(FS ~ STS, data = df,
xlab = "Standardized total score",
ylab = "Factor score")
Rasch Item Response Theory model
Item Response Theory (IRT) models are mixed-effect regression models in which student ability (theta) is assumed to be a random effect and is estimated together with item paramters. Ability (theta) is often assumed to follow normal distibution.
In Rasch IRT model, (Rasch, 1960) all items are assumed to have the same slope in inflection point – the same discrimination a which is fixed to value of 1. Items can differ in location of their inflection point – in item difficulty b.
Equation
$$\mathrm{P}\left(Y_{ij} = 1\vert \theta_{i}, b_{j} \right) = \frac{e^{\left(\theta_{i}-b_{j}\right) }}{1+e^{\left(\theta_{i}-b_{j}\right) }} $$Item characteristic curves
Download figureItem information curves
Download figureTest information function
Download figureTable of parameters with item fit statistics
Estimates of parameters are completed by SX2 item fit statistics (Ames & Penfield, 2015)
Scatter plot of factor scores and standardized total scores
Download figureWright map
Wright map (Wilson, 2005; Wright & Stone, 1979), also called item-person map, is a graphical tool to display person estimates and item parameters. The person side (left) represents histogram of estimated knowledge of students. The item side (right) displays estimates of difficulty of particular items.
Download figureSelected R code
library(difNLR)
library(mirt)
library(WrightMap)
data(GMAT)
data <- GMAT[, colnames(GMAT) != "group"]
# Model
fit <- mirt(data, model = 1, itemtype = "Rasch", SE = T)
# Item Characteristic Curves
plot(fit, type = "trace", facet_items = F)
# Item Information Curves
plot(fit, type = "infotrace", facet_items = F)
# Test Information Function
plot(fit, type = "infoSE")
# Coefficients
coef(fit, simplify = TRUE)
coef(fit, IRTpars = TRUE, simplify = TRUE)
# Item fit statistics
itemfit(fit)
# Factor scores vs Standardized total scores
fs <- as.vector(fscores(fit))
sts <- as.vector(scale(apply(data, 1, sum)))
plot(fs ~ sts)
# Wright Map
b <- sapply(1:ncol(data), function(i) coef(fit)[[i]][, "d"])
wrightMap(fs, b, item.side = itemClassic)
One parameter Item Response Theory model
Item Response Theory (IRT) models are mixed-effect regression models in which student ability (theta) is assumed to be a random effect and is estimated together with item paramters. Ability (theta) is often assumed to follow normal distibution.
In 1PL IRT model, all items are assumed to have the same slope in inflection point – the same discrimination a . Items can differ in location of their inflection point – in item difficulty b.
Equation
$$\mathrm{P}\left(Y_{ij} = 1\vert \theta_{i}, a, b_{j} \right) = \frac{e^{a\left(\theta_{i}-b_{j}\right) }}{1+e^{a\left(\theta_{i}-b_{j}\right) }} $$Item characteristic curves
Download figureItem information curves
Download figureTest information function
Download figureTable of parameters with item fit statistics
Estimates of parameters are completed by SX2 item fit statistics (Ames & Penfield, 2015)
Scatter plot of factor scores and standardized total scores
Download figureWright map
Wright map (Wilson, 2005; Wright & Stone, 1979), also called item-person map, is a graphical tool to display person estimates and item parameters. The person side (left) represents histogram of estimated knowledge of students. The item side (right) displays estimates of difficulty of particular items.
Download figureSelected R code
library(difNLR)
library(mirt)
library(WrightMap)
data(GMAT)
data <- GMAT[, colnames(GMAT) != "group"]
# Model
fit <- mirt(data, model = 1, itemtype = "2PL", constrain = list((1:ncol(data)) + seq(0, (ncol(data) - 1)*3, 3)), SE = T)
# Item Characteristic Curves
plot(fit, type = "trace", facet_items = F)
# Item Information Curves
plot(fit, type = "infotrace", facet_items = F)
# Test Information Function
plot(fit, type = "infoSE")
# Coefficients
coef(fit, simplify = TRUE)
coef(fit, IRTpars = TRUE, simplify = TRUE)
# Item fit statistics
itemfit(fit)
# Factor scores vs Standardized total scores
fs <- as.vector(fscores(fit))
sts <- as.vector(scale(apply(data, 1, sum)))
plot(fs ~ sts)
# Wright Map
b <- sapply(1:ncol(data), function(i) coef(fit)[[i]][, "d"])
wrightMap(fs, b, item.side = itemClassic)
Two parameter Item Response Theory model
Item Response Theory (IRT) models are mixed-effect regression models in which student ability (theta) is assumed to be a random effect and is estimated together with item paramters. Ability (theta) is often assumed to follow normal distibution.
2PL IRT model, allows for different slopes in inflection point – different discriminations a. Items can also differ in location of their inflection point – in item difficulty b.
Equation
$$\mathrm{P}\left(Y_{ij} = 1\vert \theta_{i}, a_{j}, b_{j}\right) = \frac{e^{a_{j}\left(\theta_{i}-b_{j}\right) }}{1+e^{a_{j}\left(\theta_{i}-b_{j}\right) }} $$Item characteristic curves
Download figureItem information curves
Download figureTest information function
Download figureTable of parameters with item fit statistics
Estimates of parameters are completed by SX2 item fit statistics (Ames & Penfield, 2015)
Scatter plot of factor scores and standardized total scores
Download figureSelected R code
library(difNLR)
library(mirt)
data(GMAT)
data <- GMAT[, colnames(GMAT) != "group"]
# Model
fit <- mirt(data, model = 1, itemtype = "2PL", SE = T)
# Item Characteristic Curves
plot(fit, type = "trace", facet_items = F)
# Item Information Curves
plot(fit, type = "infotrace", facet_items = F)
# Test Information Function
plot(fit, type = "infoSE")
# Coefficients
coef(fit, simplify = TRUE)
coef(fit, IRTpars = TRUE, simplify = TRUE)
# Item fit statistics
itemfit(fit)
# Factor scores vs Standardized total scores
fs <- as.vector(fscores(fit))
sts <- as.vector(scale(apply(data, 1, sum)))
plot(fs ~ sts)
Three parameter Item Response Theory model
Item Response Theory (IRT) models are mixed-effect regression models in which student ability (theta) is assumed to be a random effect and is estimated together with item paramters. Ability (theta) is often assumed to follow normal distibution.
3PL IRT model, allows for different discriminations of items a, different item difficulties b, and allows also for nonzero left asymptote – pseudo-guessing c.
Equation
$$\mathrm{P}\left(Y_{ij} = 1\vert \theta_{i}, a_{j}, b_{j}, c_{j} \right) = c_{j} + \left(1 - c_{j}\right) \cdot \frac{e^{a_{j}\left(\theta_{i}-b_{j}\right) }}{1+e^{a_{j}\left(\theta_{i}-b_{j}\right) }} $$Item characteristic curves
Download figureItem information curves
Download figureTest information function
Download figureTable of parameters with item fit statistics
Estimates of parameters are completed by SX2 item fit statistics (Ames & Penfield, 2015)
Scatter plot of factor scores and standardized total scores
Download figureSelected R code
library(difNLR)
library(mirt)
data(GMAT)
data <- GMAT[, colnames(GMAT) != "group"]
# Model
fit <- mirt(data, model = 1, itemtype = "3PL", SE = T)
# Item Characteristic Curves
plot(fit, type = "trace", facet_items = F)
# Item Information Curves
plot(fit, type = "infotrace", facet_items = F)
# Test Information Function
plot(fit, type = "infoSE")
# Coefficients
coef(fit, simplify = TRUE)
coef(fit, IRTpars = TRUE, simplify = TRUE)
# Item fit statistics
itemfit(fit)
# Factor scores vs Standardized total scores
fs <- as.vector(fscores(fit))
sts <- as.vector(scale(apply(data, 1, sum)))
plot(fs ~ sts)
Item Response Theory model selection
Item Response Theory (IRT) models are mixed-effect regression models in which student ability (theta) is assumed to be a random effect and is estimated together with item paramters. Ability (theta) is often assumed to follow normal distibution.
IRT models can be compared by several information criterions:
- AIC is the Akaike information criterion (Akaike, 1974),
- AICc is AIC with a correction for finite sample size,
- SABIC is the Sample-sized adjusted BIC criterion,
- BIC is the Bayesian information criterion (Schwarz, 1978).
Another approach to compare IRT models can be likelihood ratio chi-squared test. Significance level is set to 0.05.
Table of comparison statistics
Row BEST indicates which model has the lowest value of criterion, or is the largest significant model by likelihood ratio test.
Selected R code
library(difNLR)
library(mirt)
data(GMAT)
data <- GMAT[, colnames(GMAT) != "group"]
# 1PL IRT model
fit1PL <- mirt(data, model = 1, itemtype = "3PL", SE = T)
# 2PL IRT model
fit2PL <- mirt(data, model = 1, itemtype = "2PL")
# 3PL IRT model
fit3PL <- mirt(data, model = 1, itemtype = "3PL")
# Comparison
anova(fit1PL, fit2PL)
anova(fit2PL, fit3PL)
Bock's nominal Item Response Theory model
The nominal response model (NRM) was introduced by Bock (1972) as a way to model responses to items with two or more nominal categories. This model is suitable for multiple-choice items with no particular ordering of distractors. The correct answer represent the highest category, in terms of the measured latent trait.
Equation
For K possible test choices is the probability of the choice k for person i with latent trait \(\theta\) in item j given by the following equation: $$\mathrm{P}(Y_{ij} = k|\theta_i, a_{j1}, al_{j(l-1)}, d_{j(l-1)}, l = 1, \dots, K) = \frac{e^{(ak_{j(k-1)} * a_{j1} * \theta_i + d_{j(k-1)})}}{\sum_l e^{(al_{j(l-1)} * a_{j1} * \theta_i + d_{j(l-1)})}}$$Item characteristic curves
Download figureItem information curves
Download figureTest information function
Download figureTable of parameters
Scatter plot of factor scores and standardized total scores
Download figureSelected R code
library(difNLR)
library(mirt)
data(GMAT)
data <- GMAT[, colnames(GMAT) != "group"]
# Model
fit <- mirt(data, model = 1, itemtype = "nominal")
# Item Characteristic Curves
plot(fit, type = "trace", facet_items = F)
# Item Information Curves
plot(fit, type = "infotrace", facet_items = F)
# Test Information Function
plot(fit, type = "infoSE")
# Coefficients
coef(fit, simplify = TRUE)
coef(fit, IRTpars = TRUE, simplify = TRUE)
# Factor scores vs Standardized total scores
fs <- as.vector(fscores(fit))
sts <- as.vector(scale(apply(data, 1, sum)))
plot(fs ~ sts)
Total scores
DIF is not about total scores! Two groups may have the same distribution of total scores, yet, some item may function differently for two groups. Also, one of the groups may have signifficantly lower total score, yet, it may happen that there is no DIF item!
Summary of total scores for groups
Histograms of total scores for groups
For selected cut-score, blue part of histogram shows students with total score above the cut-score, grey column shows students with Total Score equal to cut-score and red part of histogram shows students below the cut-score.
Download figure Download figureSelected R code
library(difNLR)
data <- GMAT[, 1:20]
group <- GMAT[, "group"]
# Summary table
sc_zero <- apply(data[group == 0, ], 1, sum); summary(sc_zero) # total scores of reference group
sc_one <- apply(data[group == 1, ], 1, sum); summary(sc_one) # total scores of focal group
# Histograms
hist(sc_zero, breaks = 0:20)
hist(sc_one, breaks = 0:20)
Delta plot
Delta plot (Angoff & Ford, 1973) compares the proportions of correct answers per item in the two groups. It displays non-linear transformation of these proportions using quantiles of standard normal distributions (so called delta scores) for each item for the two genders in a scatterplot called diagonal plot or delta plot (see Figure). Item is under suspicion of DIF if the delta point considerably departs from the diagonal. The detection threshold is either fixed to value 1.5 or based on bivariate normal approximation (Magis & Facon, 2012).
Selected R code
library(deltaPlotR)
library(difNLR)
data(GMAT)
data <- GMAT[, 1:20]
group <- GMAT[, "group"]
# Delta scores with fixed threshold
deltascores <- deltaPlot(data.frame(data, group), group = "group",
focal.name = 1, thr = 1.5)
deltascores
# Delta plot
diagPlot(deltascores, thr.draw = T)
# Delta scores with normal threshold
deltascores <- deltaPlot(data.frame(data, group), group = "group",
focal.name = 1, thr = "norm")
deltascores
# Delta plot
diagPlot(deltascores, thr.draw = T)
Mantel-Haenszel test
Mantel-Haenszel test is DIF detection method based on contingency tables that are calculated for each level of total score (Mantel & Haenszel, 1959).
Selected R code
library(difNLR)
library(difR)
data(GMAT)
data <- GMAT[, 1:20]
group <- GMAT[, "group"]
# Mantel-Haenszel test
fit <- difMH(Data = data, group = group, focal.name = 1,
p.adjust.method = "BH")
fit
Mantel-Haenszel test
Mantel-Haenszel test is DIF detection method based on contingency tables that are calculated for each level of total score (Mantel & Haenszel, 1959).
Contingency tables and odds ratio calculation
Selected R code
library(difNLR)
library(difR)
data(GMAT)
data <- GMAT[, 1:20]
group <- GMAT[, "group"]
# Contingency table for item 1 and score 12
df <- data.frame(data[, 1], group)
colnames(df) <- c("Answer", "Group")
df$Answer <- relevel(factor(df$Answer, labels = c("Incorrect", "Correct")), "Correct")
df$Group <- factor(df$Group, labels = c("Reference Group", "Focal Group"))
score <- apply(data, 1, sum)
df <- df[score == 12, ]
tab <- dcast(data.frame(xtabs(~ Group + Answer, data = df)),
Group ~ Answer,
value.var = "Freq",
margins = T,
fun = sum)
tab
# Mantel-Haenszel estimate of OR
fit <- difMH(Data = data, group = group, focal.name = 1,
p.adjust.method = "BH")
fit$alphaMH
Logistic regression on total scores
Logistic regression allows for detection of uniform and non-uniform DIF (Swaminathan & Rogers, 1990) by adding a group specific intercept b2 (uniform DIF) and group specific interaction b3 (non-uniform DIF) into model and by testing for their significance.
Equation
$$\mathrm{P}\left(Y_{ij} = 1 | X_i, G_i, b_0, b_1, b_2, b_3\right) = \frac{e^{b_0 + b_1 X_i + b_2 G_i + b_3 X_i G_i}}{1+e^{b_0 + b_1 X_i + b_2 G_i + b_3 X_i G_i}} $$Selected R code
library(difNLR)
library(difR)
data(GMAT)
data <- GMAT[, 1:20]
group <- GMAT[, "group"]
# Logistic regression DIF detection method
fit <- difLogistic(Data = data, group = group, focal.name = 1,
type = "both",
p.adjust.method = "BH")
fit
Logistic regression on total scores
Logistic regression allows for detection of uniform and non-uniform DIF by adding a group specific intercept b2 (uniform DIF) and group specific interaction b3 (non-uniform DIF) into model and by testing for their significance.
Plot with estimated DIF logistic curve
Points represent proportion of correct answer with respect to standardized total score. Their size is determined by count of respondents who answered item correctly.
NOTE: Plots and tables are based on DIF logistic procedure without any correction method.
Equation
$$\mathrm{P}\left(Y_{ij} = 1 | X_i, G_i, b_0, b_1, b_2, b_3\right) = \frac{e^{b_0 + b_1 X_i + b_2 G_i + b_3 X_i G_i}}{1+e^{b_0 + b_1 X_i + b_2 G_i + b_3 X_i G_i}} $$Table of parameters
Selected R code
library(difNLR)
library(difR)
data(GMAT)
data <- GMAT[, 1:20]
group <- GMAT[, "group"]
# Logistic regression DIF detection method
fit <- difLogistic(Data = data, group = group, focal.name = 1,
type = "both",
p.adjust.method = "BH")
fit
# Plot of characteristic curve for item 1
plotDIFLogistic(data, group,
type = "both",
item = 1,
IRT = F,
p.adjust.method = "BH")
# Coefficients
fit$logitPar
Logistic regression on standardized total scores with IRT parameterization
Logistic regression allows for detection of uniform and non-uniform DIF (Swaminathan & Rogers, 1990) by adding a group specific intercept bDIF (uniform DIF) and group specific interaction aDIF (non-uniform DIF) into model and by testing for their significance.
Equation
$$\mathrm{P}\left(Y_{ij} = 1 | Z_i, G_i, a_j, b_j, a_{\text{DIF}j}, b_{\text{DIF}j}\right) = \frac{e^{\left(a_j + a_{\text{DIF}j} G_i\right) \left(Z_i -\left(b_j + b_{\text{DIF}j} G_i\right)\right)}}{1+e^{\left(a_j + a_{\text{DIF}j} G_i\right) \left(Z_i -\left(b_j + b_{\text{DIF}j} G_i\right)\right)}} $$Selected R code
library(difNLR)
library(difR)
data(GMAT)
data <- GMAT[, 1:20]
group <- GMAT[, "group"]
scaled.score <- scale(score)
# Logistic regression DIF detection method
fit <- difLogistic(Data = data, group = group, focal.name = 1,
type = "both",
match = scaled.score,
p.adjust.method = "BH")
fit
Logistic regression on standardized total scores with IRT parameterization
Logistic regression allows for detection of uniform and non-uniform DIF by adding a group specific intercept bDIF (uniform DIF) and group specific interaction aDIF (non-uniform DIF) into model and by testing for their significance.
Plot with estimated DIF logistic curve
Points represent proportion of correct answer with respect to standardized total score. Their size is determined by count of respondents who answered item correctly.
NOTE: Plots and tables are based on DIF logistic procedure without any correction method.
Equation
$$\mathrm{P}\left(Y_{ij} = 1 | Z_i, G_i, a_j, b_j, a_{\text{DIF}j}, b_{\text{DIF}j}\right) = \frac{e^{\left(a_j + a_{\text{DIF}j} G_i\right)\left(Z_i -\left(b_j + b_{\text{DIF}j} G_i\right)\right)}} {1+e^{\left(a_j + a_{\text{DIF}j} G_i\right)\left(Z_i -\left(b_j + b_{\text{DIF}j} G_i\right)\right)}} $$Table of parameters
Selected R code
library(difNLR)
library(difR)
data(GMAT)
data <- GMAT[, 1:20]
group <- GMAT[, "group"]
scaled.score <- scale(score)
# Logistic regression DIF detection method
fit <- difLogistic(Data = data, group = group, focal.name = 1,
type = "both",
match = scaled.score,
p.adjust.method = "BH")
fit
# Plot of characteristic curve for item 1
plotDIFLogistic(data, group,
type = "both",
item = 1,
IRT = T,
p.adjust.method = "BH")
# Coefficients for item 1 - recalculation
coef_old <- fit$logitPar[1, ]
coef <- c()
# a = b1, b = -b0/b1, adif = b3, bdif = -(b1b2-b0b3)/(b1(b1+b3))
coef[1] <- coef_old[2]
coef[2] <- -(coef_old[1] / coef_old[2])
coef[3] <- coef_old[4]
coef[4] <- -(coef_old[2] * coef_old[3] + coef_old[1] * coef_old[4] ) /
(coef_old[2] * (coef_old[2] + coef_old[4]))
Nonlinear regression on standardized total scores
Nonlinear regression model allows for nonzero lower asymptote - pseudoguessing c. Similarly to logistic regression, also nonlinear regression allows for detection of uniform and non-uniform DIF by adding a group specific intercept bDIF (uniform DIF) and group specific interaction aDIF (non-uniform DIF) into the model and by testing for their significance.
Equation
$$\mathrm{P}\left(Y_{ij} = 1 | Z_i, G_i, a_j, b_j, c_j, a_{\text{DIF}j}, b_{\text{DIF}j}\right) = c_j + \left(1 - c_j\right) \cdot \frac{e^{\left(a_j + a_{\text{DIF}j} G_i\right)\left(Z_i -\left(b_j + b_{\text{DIF}j} G_i\right)\right)}} {1+e^{\left(a_j + a_{\text{DIF}j} G_i\right)\left(Z_i -\left(b_j + b_{\text{DIF}j} G_i\right)\right)}} $$Selected R code
library(difNLR)
data(GMAT)
Data <- GMAT[, 1:20]
group <- GMAT[, "group"]
# Nonlinear regression DIF method
fit <- difNLR(Data = Data, group = group, focal.name = 1,
model = "3PLcg", type = "both", p.adjust.method = "BH")
fit
Nonlinear regression on standardized total scores
Nonlinear regression model allows for nonzero lower asymptote - pseudoguessing c. Similarly to logistic regression, also nonlinear regression allows for detection of uniform and non-uniform DIF (Drabinova & Martinkova, 2016) by adding a group specific intercept bDIF (uniform DIF) and group specific interaction aDIF (non-uniform DIF) into the model and by testing for their significance.
Plot with estimated DIF nonlinear curve
Points represent proportion of correct answer with respect to standardized total score. Their size is determined by count of respondents who answered item correctly.
Equation
$$\mathrm{P}\left(Y_{ij} = 1 | Z_i, G_i, a_j, b_j, c_j, a_{\text{DIF}j}, b_{\text{DIF}j}\right) = c_j + \left(1 - c_j\right) \cdot \frac{e^{\left(a_j + a_{\text{DIF}j} G_i\right)\left(Z_i -\left(b_j + b_{\text{DIF}j} G_i\right)\right)}} {1+e^{\left(a_j + a_{\text{DIF}j} G_i\right)\left(Z_i -\left(b_j + b_{\text{DIF}j} G_i\right)\right)}} $$Table of parameters
Selected R code
library(difNLR)
data(GMAT)
Data <- GMAT[, 1:20]
group <- GMAT[, "group"]
# Nonlinear regression DIF method
fit <- difNLR(Data = Data, group = group, focal.name = 1,
model = "3PLcg", type = "both", p.adjust.method = "BH")
# Plot of characteristic curve of item 1
plot(fit, item = 1)
# Coefficients
fit$nlrPAR
Lord test for IRT models
Lord test (Lord, 1980) is based on IRT model (1PL, 2PL, or 3PL with the same guessing). It uses the difference between item parameters for the two groups to detect DIF. In statistical terms, Lord statistic is equal to Wald statistic.
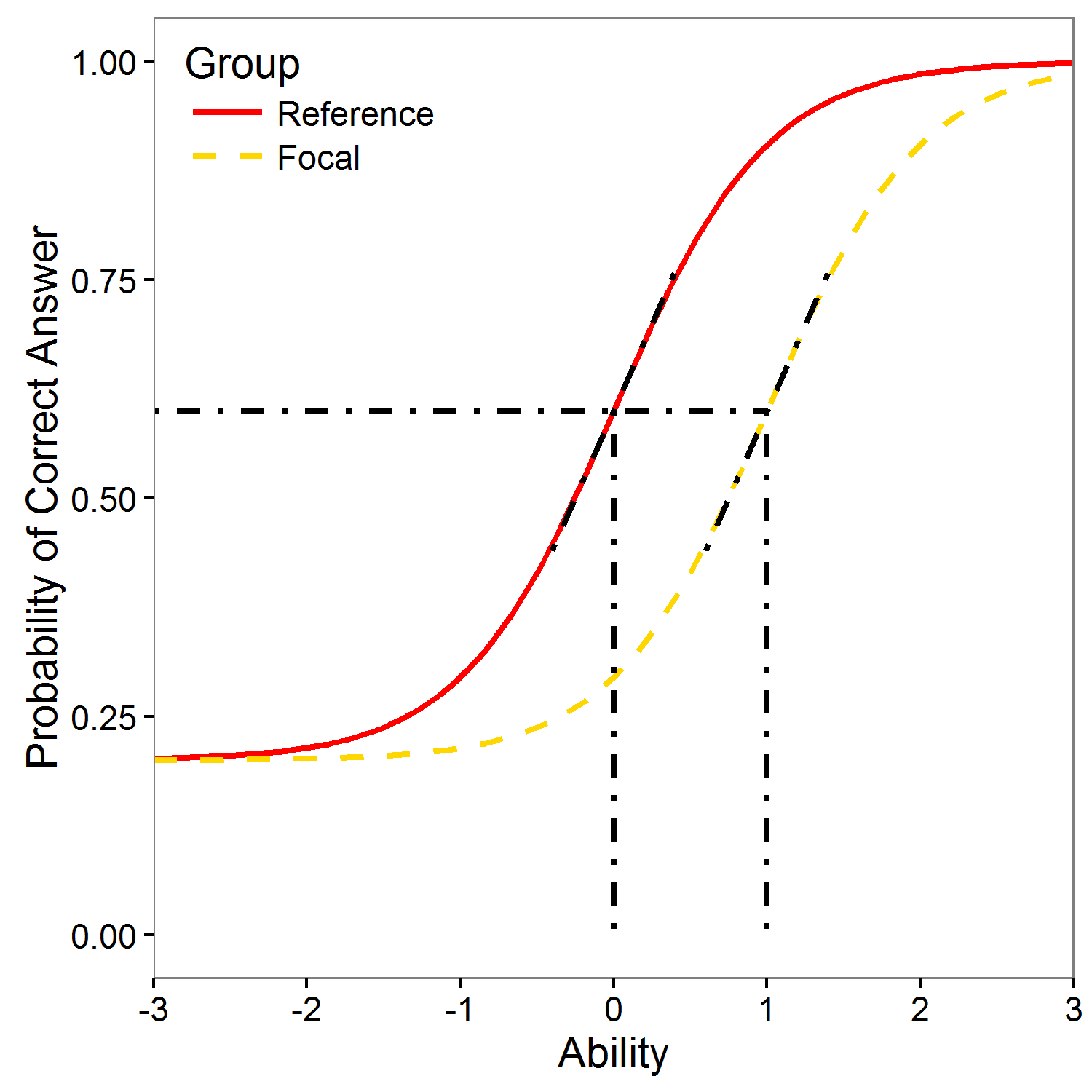
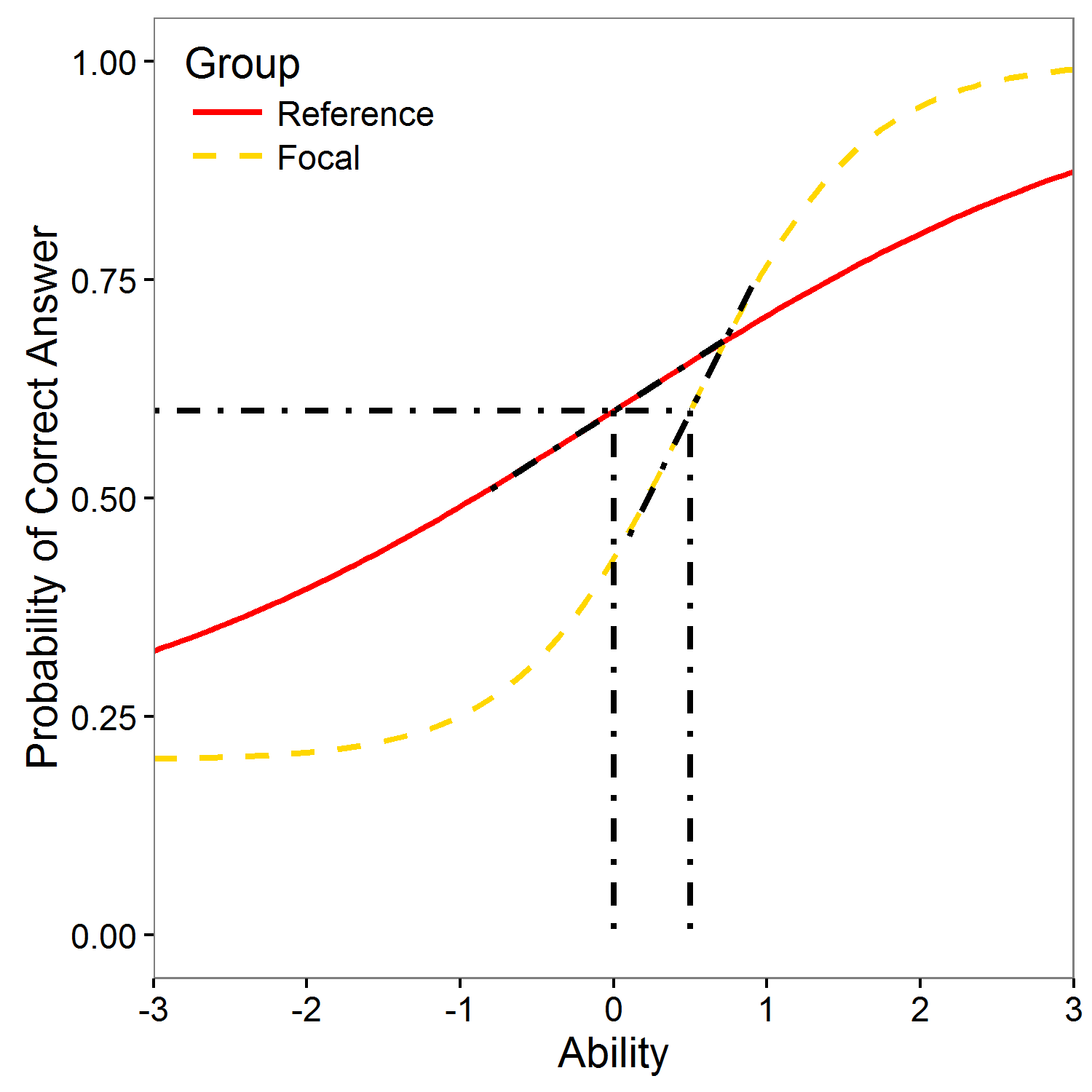
Selected R code
library(difNLR)
library(difR)
data(GMAT)
data <- GMAT[, 1:20]
group <- GMAT[, "group"]
# 2PL IRT MODEL
fit <- difLord(Data = data, group = group, focal.name = 1,
model = "2PL",
p.adjust.method = "BH")
fit
Lord test for IRT models
Lord test (Lord, 1980) is based on IRT model (1PL, 2PL, or 3PL with the same guessing). It uses the difference between item parameters for the two groups to detect DIF. In statistical terms, Lord statistic is equal to Wald statistic.
Plot with estimated DIF characteristic curve
NOTE: Plots and tables are based on larger DIF IRT model.
Equation
Table of parameters
Selected R code
library(difNLR)
library(difR)
data(GMAT)
data <- GMAT[, 1:20]
group <- GMAT[, "group"]
# 2PL IRT MODEL
fit <- difLord(Data = data, group = group, focal.name = 1,
model = "2PL",
p.adjust.method = "BH")
fit
# Coefficients for item 1
tab_coef <- fit$itemParInit[c(1, ncol(data) + 1), 1:2]
# Plot of characteristic curve of item 1
plotDIFirt(parameters = tab_coef, item = 1)
Raju test for IRT models
Raju test (Raju, 1988, 1990) is based on IRT model (1PL, 2PL, or 3PL with the same guessing). It uses the area between the item charateristic curves for the two groups to detect DIF.
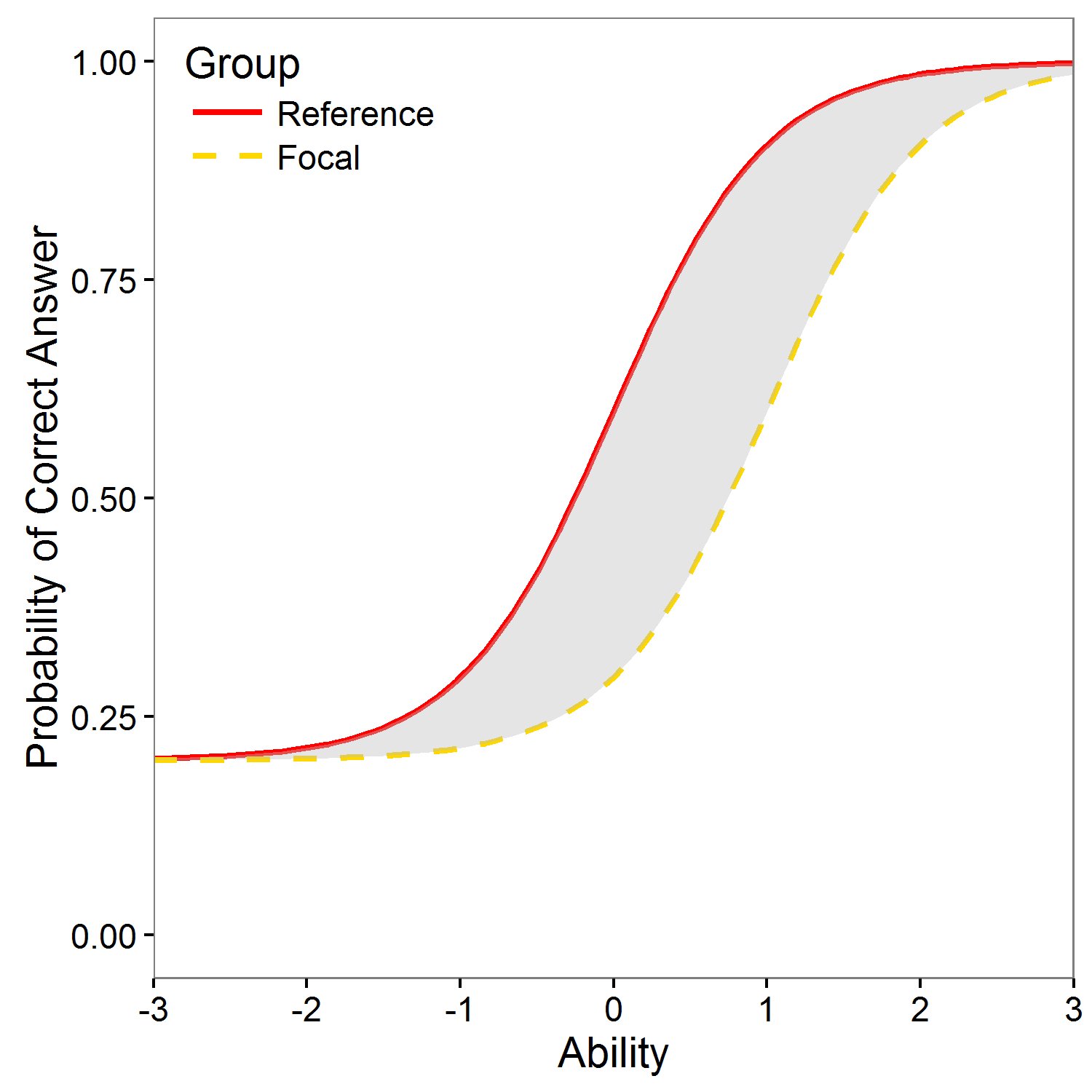
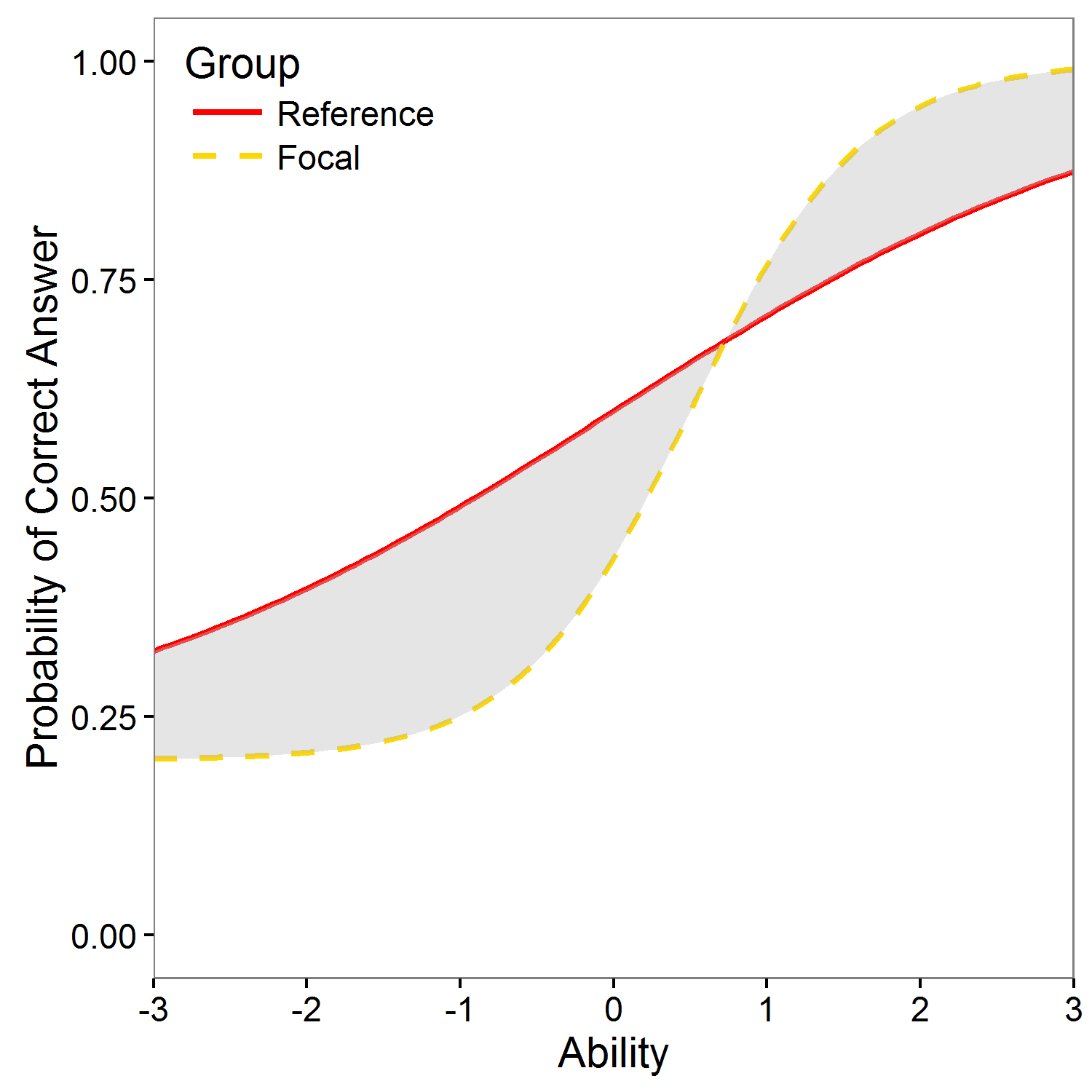
Selected R code
library(difNLR)
library(difR)
data(GMAT)
data <- GMAT[, 1:20]
group <- GMAT[, "group"]
# 2PL IRT MODEL
fit <- difRaju(Data = data, group = group, focal.name = 1,
model = "2PL",
p.adjust.method = "BH")
fit
Raju test for IRT models
Raju test (Raju, 1988, 1990) is based on IRT model (1PL, 2PL, or 3PL with the same guessing). It uses the area between the item charateristic curves for the two groups to detect DIF.
Plot with estimated DIF characteristic curve
NOTE: Plots and tables are based on larger DIF IRT model.
Equation
Table of parameters
Selected R code
library(difNLR)
library(difR)
data(GMAT)
data <- GMAT[, 1:20]
group <- GMAT[, "group"]
# 2PL IRT MODEL
fit <- difRaju(Data = data, group = group, focal.name = 1,
model = "2PL",
p.adjust.method = "BH")
fit
# Coefficients for item 1
tab_coef <- fit$itemParInit[c(1, ncol(data) + 1), 1:2]
# Plot of characteristic curve of item 1
plotDIFirt(parameters = tab_coef, item = 1, test = "Raju")
Differential Distractor Functioning with multinomial log-linear regression Model
Differential Distractor Functioning (DDF) occurs when people from different groups but with the same knowledge have different probability of selecting at least one distractor choice. DDF is here examined by Multinomial Log-linear Regression model with Z-score and group membership as covariates.
Equation
For K possible test choices is the probability of the correct answer for person i with standardized total score Z and group membership G in item j given by the following equation:
$$\mathrm{P}(Y_{ij} = K|Z_i, G_i, b_{jl0}, b_{jl1}, b_{jl2}, b_{jl3}, l = 1, \dots, K-1) = \frac{1}{1 + \sum_l e^{\left( b_{il0} + b_{il1} Z + b_{il2} G + b_{il3} Z:G\right)}}$$The probability of choosing distractor k is then given by:
$$\mathrm{P}(Y_{ij} = k|Z_i, G_i, b_{jl0}, b_{jl1}, b_{jl2}, b_{jl3}, l = 1, \dots, K-1) = \frac{e^{\left( b_{jk0} + b_{jk1} Z_i + b_{jk2} G_i + b_{jk3} Z_i:G_i\right)}} {1 + \sum_l e^{\left( b_{jl0} + b_{jl1} Z_i + b_{jl2} G_i + b_{jl3} Z_i:G_i\right)}}$$Selected R code
library(difNLR)
data(GMATtest, GMATkey)
Data <- GMATtest[, 1:20]
group <- GMATtest[, "group"]
key <- GMATkey
# DDF with difNLR package
fit <- ddfMLR(Data, group, focal.name = 1, key, type = "both",
p.adjust.method = "BH")
fit
Differential Distractor Functioning with multinomial log-linear regression model
Differential Distractor Functioning (DDF) occurs when people from different groups but with the same knowledge have different probability of selecting at least one distractor choice. DDF is here examined by Multinomial Log-linear Regression model with Z-score and group membership as covariates.
Plot with estimated DDF curves
Points represent proportion of selected answer with respect to standardized total score. Size of points is determined by count of respondents who chose particular answer.
Equation
Table of parameters
Selected R code
library(difNLR)
data(GMATtest, GMATkey)
Data <- GMATtest[, 1:20]
group <- GMATtest[, "group"]
key <- GMATkey
# DDF with difNLR package
fit <- ddfMLR(Data, group, focal.name = 1, key, type = "both",
p.adjust.method = "BH")
# Estimated coefficients of item 1
fit$mlrPAR[[1]]
Differential Item Functioning / Item Fairness
Differential item functioning (DIF) occurs when people from different groups (commonly gender or ethnicity) with the same underlying true ability have a different probability of answering the item correctly. If item functions differently for two groups, it is potentially unfair. In general, two type of DIF can be recognized: if the item has different difficulty for given two groups with the same discrimination, uniform DIF is present (left figure). If the item has different discrimination and possibly also different difficulty for given two groups, non-uniform DIF is present (right figure)
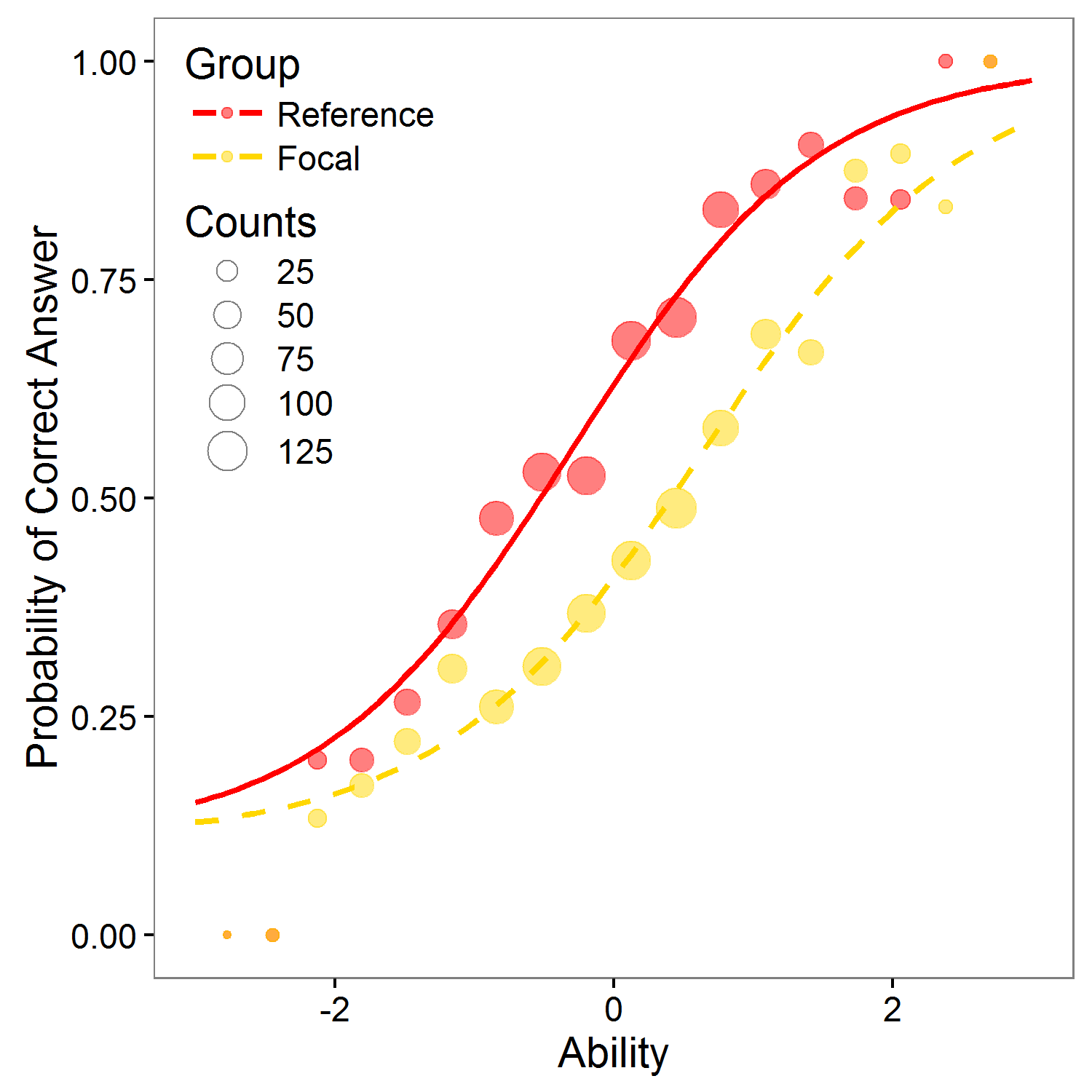
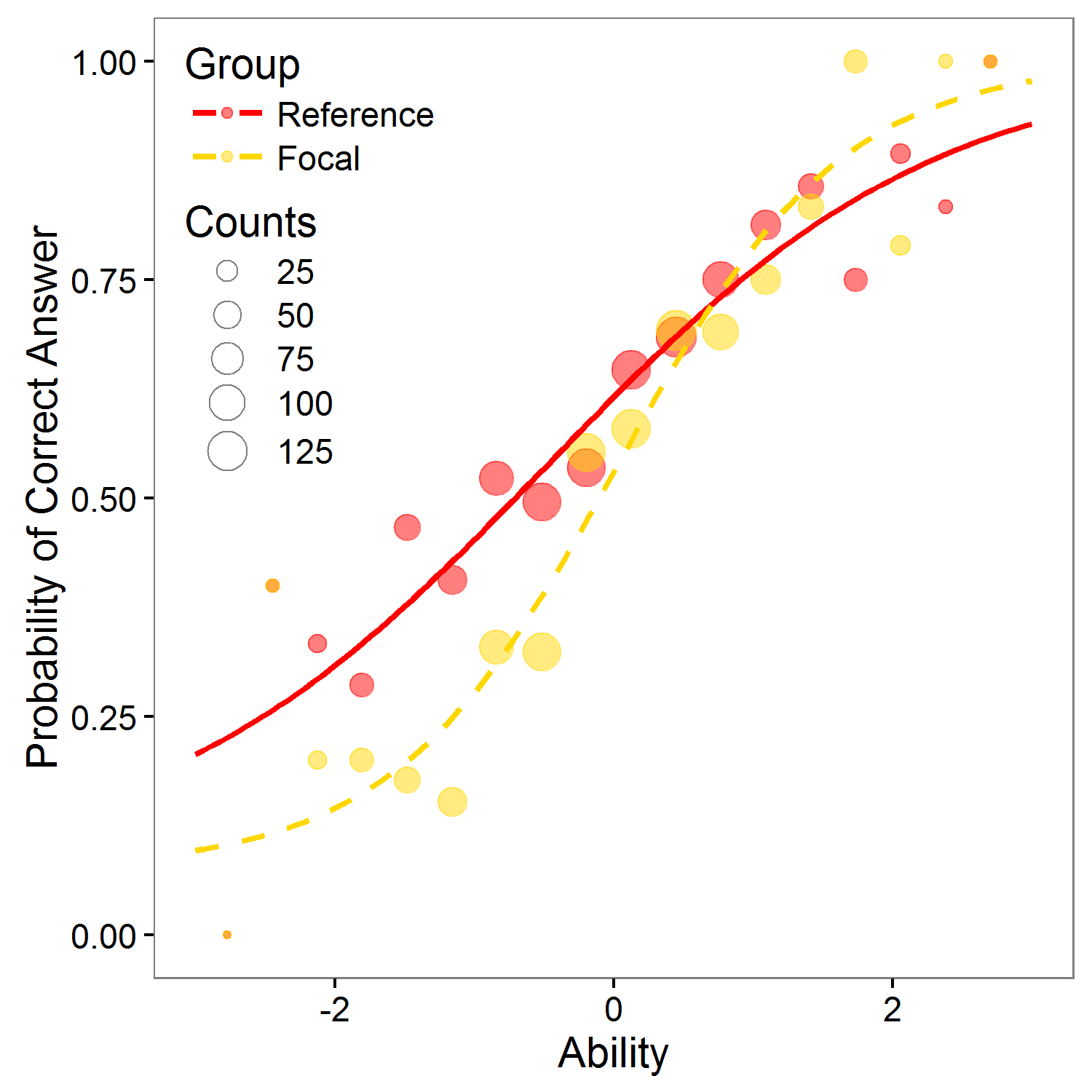
Download report
This shiny app also offers an option to download a report in HTML or PDF format.
PDF report creation requires latest version of MiKTeX (or other TeX distribution). If you don't have the latest installation, please, use the HTML report.
Warning : download of Reports takes some time. Please, be patient.
References
Akaike, H. (1974). A New Look at the Statistical Model Identification. IEEE Transactions on Automatic Control, 19(6), 716-723. See online.
Ames, A. J., & Penfield, R. D. (2015). An NCME Instructional Module on Item-Fit Statistics for Item Response Theory Models. Educational Measurement: Issues and Practice, 34(3), 39-48. See online.
Angoff, W. H., & Ford, S. F. (1973). Item-Race Interaction on a Test of Scholastic Aptitude. Journal of Educational Measurement, 10(2), 95-105.
Bock, R. D. (1972). Estimating Item Parameters and Latent Ability when Responses Are Scored in Two or More Nominal Categories. Psychometrika, 37(1), 29-51. See online.
Cronbach, L. J. (1951). Coefficient alpha and the internal structure of tests. psychometrika, 16(3), 297-334.
Drabinova, A., & Martinkova, P. (2016). Detection of Differential Item Functioning Based on Non-Linear Regression. Technical Report V-1229 .
Lord, F. M. (1980). Applications of Item Response Theory to Practical Testing Problems. Routledge.
Magis, D., & Facon, B. (2012). Angoff's delta method revisited: Improving DIF detection under small samples. British Journal of Mathematical and Statistical Psychology, 65(2), 302-321.
Mantel, N., & Haenszel, W. (1959). Statistical Aspects of the Analysis of Data from Retrospective Studies. Journal of the National Cancer Institute, 22 (4), 719-748.
Swaminathan, H., & Rogers, H. J. (1990). Detecting Differential Item Functioning Using Logistic Regression Procedures. Journal of Educational Measurement, 27(4), 361-370.
Raju, N. S. (1988). The Area between Two Item Characteristic Curves. Psychometrika, 53 (4), 495-502.
Raju, N. S. (1990). Determining the Significance of Estimated Signed and Unsigned Areas between Two Item Response Functions. Applied Psychological Measurement, 14 (2), 197-207.
Rasch, G. (1960) Probabilistic Models for Some Intelligence and Attainment Tests. Copenhagen: Paedagogiske Institute.
Schwarz, G. (1978). Estimating the Dimension of a Model. The Annals of Statistics, 6(2), 461-464. See online.
Wilson, M. (2005). Constructing Measures: An Item Response Modeling Approach.
Wright, B. D., & Stone, M. H. (1979). Best Test Design. Chicago: Mesa Press.