ShinyItemAnalysis provides analysis of educational tests (such as admission tests)
and its items. For demonstration purposes, 20-item dataset
GMAT
from
R
library(difNLR)
is used. You can change the dataset
(and try your own one) on page
Data.
Analysis of Total Scores
Summary Table
Histogram of Total Score
For selected cut-score, blue part of histogram shows students with total score above the cut-score, grey column shows students with Total Score equal to cut-score and red part of histogram shows students below the cut-score.
Table by Score
Traditional Item Analysis
Traditional item analysis uses proportions of correct answers or correlations to estimate item properties.
Item Difficulty/Discrimination Graph
Displayed is difficulty (red) and discrimination (blue) for all items. Items are ordered by difficulty.
Difficulty of items is estimated as percent of students who answered correctly to that item.
Discrimination is described by difference of percent correct in upper and lower third of students (Upper-Lower Index, ULI). By rule of thumb it should not be lower than 0.2 (borderline in the plot), except for very easy or very difficult items.
Traditional Item Analysis Table
Explanation:Difficulty Difficulty of item is estimated as percent of students who answered correctly to that item. SD standard deviation, RIT Pearson correlation between item and Total score, RIR Pearson correlation between item and rest of items, ULI - Upper-Lower Index, Alpha Drop - Cronbach's alpha of test without given item.
Traditional item analysis uses proportions of correct answers or correlations to estimate item properties.
Distractor Analysis
In distractor analysis, we are interested in how test takers select the correct answer and how the distractors (wrong answers) were able to function effectively by drawing the test takers away from the correct answer.
Distractors Plot
Table with Counts
Table with Proportions
Logistic Regression on Total Scores
Various regression models may be fitted to describe item properties in more detail. Logistic regression can model dependency of probability of correct answer on total score by s-shaped logistic curve. Parameter b0 describes horizontal position of the fitted curve, parameter b1 describes its slope.
Plot with estimated logistic curve
Equation
$$\mathrm{P}(Y = 1|X, b_0, b_1) = \mathrm{E}(Y|X, b_0, b_1) = \frac{e^{\left( b_{0} + b_1 X\right)}}{1+e^{\left( b_{0} + b_1 X\right) }} $$Table of parametres
Logistic Regression on Standardized Total Scores
Various regression models may be fitted to describe item properties in more detail. Logistic regression can model dependency of probability of correct answer on standardized total score (Z-score) by s-shaped logistic curve. Parameter b0 describes horizontal position of the fitted curve (difficulty), parameter b1 describes its slope at inflection point (discrimination).
Plot with estimated logistic curve
Equation
$$\mathrm{P}(Y = 1|Z, b_0, b_1) = \mathrm{E}(Y|Z, b_0, b_1) = \frac{e^{\left( b_{0} + b_1 Z\right) }}{1+e^{\left( b_{0} + b_1 Z\right) }} $$Table of parametres
Logistic Regression on Standardized Total Scores
Various regression models may be fitted to describe item properties in more detail. Logistic regression can model dependency of probability of correct answer on standardized total score (Z-score) by s-shaped logistic curve. Note change in parametrization - the IRT parametrization used here corresponds to the parametrization used in IRT models. Parameter b describes horizontal position of the fitted curve (difficulty), parameter a describes its slope at inflection point (discrimination).
Plot with estimated logistic curve
Equation
$$\mathrm{P}(Y = 1|Z, a, b) = \mathrm{E}(Y|Z, a, b) = \frac{e^{ a\left(Z - b\right) }}{1+e^{a\left(Z - b\right)}} $$Table of parametres
Nonlinear Regression on Standardized Total Scores
Various regression models may be fitted to describe item properties in more detail. Nonlinear regression can model dependency of probability of correct answer on standardized total score (Z-score) by s-shaped logistic curve. The IRT parametrization used here corresponds to the parametrization used in IRT models. Parameter b describes horizontal position of the fitted curve (difficulty), parameter a describes its slope at inflection point (discrimination). This model allows for nonzero lower left asymptote c (pseudo-guessing).
Plot with estimated nonlinear curve
Equation
$$\mathrm{P}(Y = 1|Z, b_0, b_1, c) = \mathrm{E}(Y|Z, b_0, b_1, c) = c + \left( 1-c \right) \cdot \frac{e^{a\left(Z-b\right) }}{1+e^{a\left(Z-b\right) }} $$Table of parametres
Multinomial Regression on Standardized Total Scores
Various regression models may be fitted to describe item properties in more detail. Multinomial regression allows for simultaneous modelling of probability of choosing given distractors on standardized total score (Z-score).
Plot with estimated curves of multinomial regression
Equation
Table of parametres
One Parameter Item Response Theory Model
Item Response Theory (IRT) models are mixed-effect regression models in which student ability (theta) is assumed to be a random effect and is estimated together with item paramters. Ability (theta) is often assumed to follow normal distibution.
In 1PL IRT model, all items are assumed to have the same slope in inflection point – the same discrimination a. Items can differ in location of their inflection point – in item difficulty b. More restricted version of this model, the Rasch model, assumes discrimination a is equal to 1.
Equation
$$\mathrm{P}\left(Y_{ij} = 1\vert \theta_{i}, a, b_{j} \right) = \frac{e^{a\left(\theta_{i}-b_{j}\right) }}{1+e^{a\left(\theta_{i}-b_{j}\right) }} $$Item Characteristic Curves
Item information curves
Test information function
Table of coefficients
Factor Scores vs. Standardized Total Scores
Two Parameter Item Response Theory Model
Item Response Theory (IRT) models are mixed-effect regression models in which student ability (theta) is assumed to be a random effect and is estimated together with item paramters. Ability (theta) is often assumed to follow normal distibution.
2PL IRT model, allows for different slopes in inflection point – different discriminations a. Items can also differ in location of their inflection point – in item difficulty b.
Equation
$$\mathrm{P}\left(Y_{ij} = 1\vert \theta_{i}, a_{j}, b_{j}\right) = \frac{e^{a_{j}\left(\theta_{i}-b_{j}\right) }}{1+e^{a_{j}\left(\theta_{i}-b_{j}\right) }} $$Item Characteristic Curves
Item information curves
Test information function
Table of coefficients
Factor Scores vs. Standardized Total Scores
Three Parameter Item Response Theory Model
Item Response Theory (IRT) models are mixed-effect regression models in which student ability (theta) is assumed to be a random effect and is estimated together with item paramters. Ability (theta) is often assumed to follow normal distibution.
3PL IRT model, allows for different discriminations of items a, different item difficulties b, and allows also for nonzero left asymptote – pseudo-guessing c.
Equation
$$\mathrm{P}\left(Y_{ij} = 1\vert \theta_{i}, a_{j}, b_{j}, c_{j} \right) = c_{j} + \left(1 - c_{j}\right) \cdot \frac{e^{a_{j}\left(\theta_{i}-b_{j}\right) }}{1+e^{a_{j}\left(\theta_{i}-b_{j}\right) }} $$Item characterisic curves
Item information curves
Test information function
Table of coefficients
Factor Scores vs. Standardized Total Scores
Differential Item Functioning / Item Fairness
Differential item functioning (DIF) occurs when people from different groups (commonly gender or ethnicity) with the same underlying true ability have a different probability of answering the item correctly. If item functions differently for two groups, it is potentially unfair.
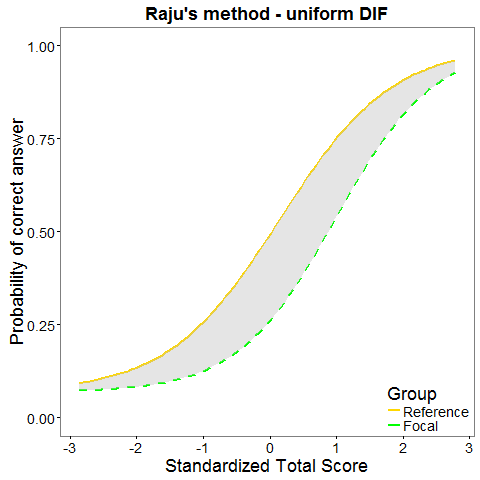
Figure 1: Uniform DIF (item has different difficulty for given two groups)
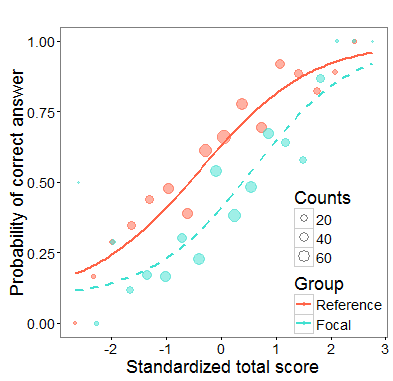
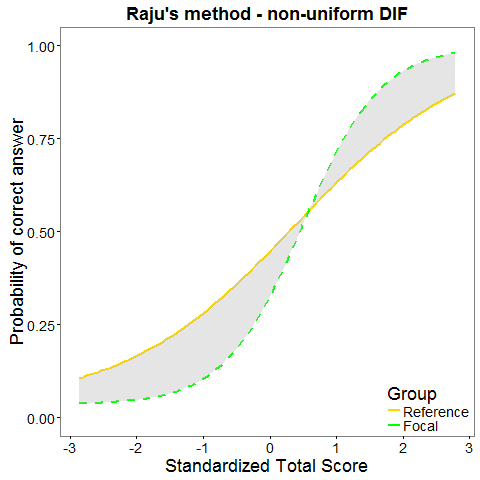
Figure 2: Non-uniform DIF (item has different discrimination and possibly also different difficulty for given two groups)
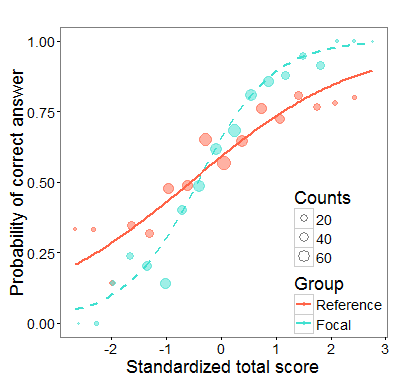
Total Scores
DIF is not about total scores! Two groups may have the same distribution of total scores, yet, some item may function differently dor the two groups. Also, one of the groups may have signifficantly lower total score, yet, it may happen that there is no DIF item!
Summary of Total Scores for Groups
Histograms of Total Scores for Groups
For selected cut-score, blue part of histogram shows students with total score above the cut-score, grey column shows students with Total Score equal to cut-score and red part of histogram shows students below the cut-score.
Delta Plot
Delta plot (Angoff and Ford, 1993) compares the proportions of correct answers per item in the two groups. It displays non-linear transformation of these proportions using quantiles of standard normal distributions (so called delta scores) for each item for the two genders in a scatterplot called diagonal plot or delta plot (see Figure). Item is under suspicion of DIF if the delta point considerably departs from the diagonal.
Logistic regression
Logistic regression allows for detection of uniform and non-uniform DIF (Swaminathan and Rogers, 1990) by adding a group specific intercept bDIF (uniform DIF) and group specific interaction aDIF (non-uniform DIF) into model and by testing for their significance.
Equation
$$\mathrm{P}\left(Y_{ij} = 1 | Z_i, G_i, a_j, b_j, a_{\text{DIF}j}, b_{\text{DIF}j}\right) = \frac{e^{\left(a_j + a_{\text{DIF}j} G_i\right) \left(Z_i -\left(b_j + b_{\text{DIF}j} G_i\right)\right)}}{1+e^{\left(a_j + a_{\text{DIF}j} G_i\right) \left(Z_i -\left(b_j + b_{\text{DIF}j} G_i\right)\right)}} $$Logistic regression
Logistic regression allows for detection of uniform and non-uniform DIF by adding a group specific intercept bDIF (uniform DIF) and group specific interaction aDIF (non-uniform DIF) into model and by testing for their significance.
DIF logistic plot
Equation
$$\mathrm{P}\left(Y_{ij} = 1 | Z_i, G_i, a_j, b_j, a_{\text{DIF}j}, b_{\text{DIF}j}\right) = \frac{e^{\left(a_j + a_{\text{DIF}j} G_i\right)\left(Z_i -\left(b_j + b_{\text{DIF}j} G_i\right)\right)}} {1+e^{\left(a_j + a_{\text{DIF}j} G_i\right)\left(Z_i -\left(b_j + b_{\text{DIF}j} G_i\right)\right)}} $$Table of parametres
Nonlinear regression
Nonlinear regression model allows for nonzero lower asymptote - pseudoguessing c. Similarly to logistic regression, also nonlinear regression allows for detection of uniform and non-uniform DIF by adding a group specific intercept bDIF (uniform DIF) and group specific interaction aDIF (non-uniform DIF) into the model and by testing for their significance.
Equation
$$\mathrm{P}\left(Y_{ij} = 1 | Z_i, G_i, a_j, b_j, c_j, a_{\text{DIF}j}, b_{\text{DIF}j}\right) = c_j + \left(1 - c_j\right) \cdot \frac{e^{\left(a_j + a_{\text{DIF}j} G_i\right)\left(Z_i -\left(b_j + b_{\text{DIF}j} G_i\right)\right)}} {1+e^{\left(a_j + a_{\text{DIF}j} G_i\right)\left(Z_i -\left(b_j + b_{\text{DIF}j} G_i\right)\right)}} $$Nonlinear regression
Nonlinear regression model allows for nonzero lower asymptote - pseudoguessing c. Similarly to logistic regression, also nonlinear regression allows for detection of uniform and non-uniform DIF (Drabinova and Martinkova, 2016) by adding a group specific intercept bDIF (uniform DIF) and group specific interaction aDIF (non-uniform DIF) into the model and by testing for their significance.
DIF NLR Plot
Equation
$$\mathrm{P}\left(Y_{ij} = 1 | Z_i, G_i, a_j, b_j, c_j, a_{\text{DIF}j}, b_{\text{DIF}j}\right) = c_j + \left(1 - c_j\right) \cdot \frac{e^{\left(a_j + a_{\text{DIF}j} G_i\right)\left(Z_i -\left(b_j + b_{\text{DIF}j} G_i\right)\right)}} {1+e^{\left(a_j + a_{\text{DIF}j} G_i\right)\left(Z_i -\left(b_j + b_{\text{DIF}j} G_i\right)\right)}} $$Table of parametres
Lord statistic
Lord statistic (Lord, 1980) is based on IRT model (1PL, 2PL, or 3PL with the same guessing). It uses the difference between item parameters for the two groups to detect DIF. In statistical terms, Lord statistic is equal to Wald statistic.
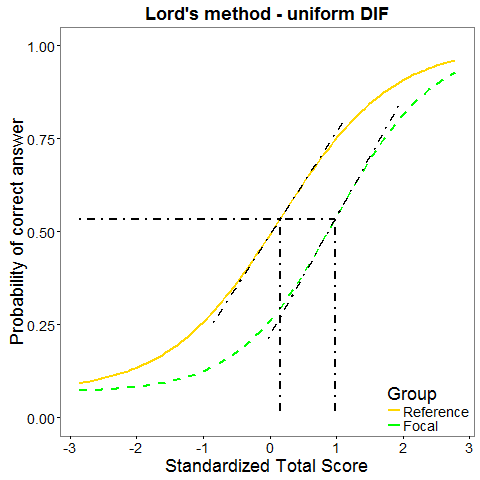
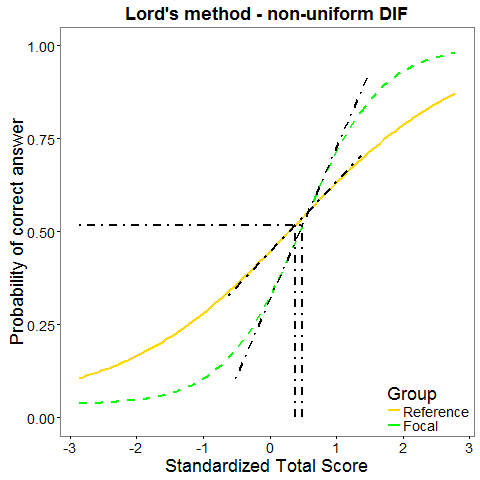
Raju statistic
Raju statistic (Raju, 1988, 1990) is based on IRT model (1PL, 2PL, or 3PL with the same guessing). It uses the area between the item charateristic curves for the two groups to detect DIF.
Data
For demonstration purposes, 20-item dataset
GMAT
and datasets
GMATkey
and
GMATgroups
from
R
library(difNLR)
are used. On this page, you may select your own dataset (see below).
To return to demonstration dataset, refresh this page in your browser
(F5)
.
Used dataset
GMAT
is generated based on parameters of real Graduate Management
Admission Test (GMAT) data set (Kingston et al., 1985). However, first two items were
generated to function differently in non-uniform and uniform way respectively.
The data set represents responses of 1,000 subjects to multiple-choice test of 20 items.
Upload your own datasets
Main dataset should contain responses of individual students (rows) to given items (collumns). Header may contain item names, no row names should be included. If responses are in ABC format, the key provides correct respomse for each item. If responses are scored 0-1, key is vecor of 1s.
Data Specification
Data Check (first 6 respondents only)
Key (correct answers)
Scored Test
ShinyItemAnalysis Version 0.2
ShinyItemAnalysis Version 0.1 is available here.
Description
ShinyItemAnalysis provides analysis of tests and their items. It is based on the Shiny R package.
Data
For demonstration purposes, practice dataset from
library(difNLR)
is used.
On page
Data
you may select your own dataset
List of Packages Used
library(CTT)
library(deltaPlotR)
library(difNLR)
library(ggplot2)
library(gridExtra)
library(ltm)
library(moments)
library(nnet)
library(psychometric)
library(reshape2)
library(shiny)
library(shinyAce)
Authors

Patricia Martinkova, Institute of Computer Science, Czech Academy of Sciences


Adela Drabinova
Bug ReportsIf you discover a problem with this application please contact the project maintainer at martinkova(at)cs.cas.cz
AcknowledgmentsProject was supported by grant funded by Czech Science foundation under number GJ15-15856Y
License
Copyright 2016 Patricia Martinkova, Ondrej Leder and Adela Drabinova
This program is free software you can redistribute it and or modify it under the terms of the GNU General Public License as published by the Free Software Foundation either version 3 of the License or at your option any later version.
This program is distributed in the hope that it will be useful, but WITHOUT ANY WARRANTY; without even the implied warranty of MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the GNU General Public License for more details.